The study of geoemtric dissections is not unlike the study of integration in calculus. There is some nice theory about the existence of integrals, and some useful techniques of integration, but no universal rules and no guarantees. It is the same with dissections.
We present here a couple of useful techniques for dissections. The first is the parallelogram slide or P-slide. This is a 3-piece dissection for transforming a parallelogram into another parallelogram having different side lengths but the same angles.
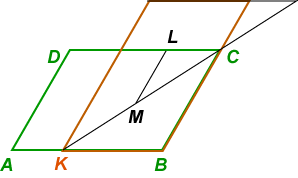
In the figure at right, we dissect the green parallelogram into the 3 pieces ADLM, LMC and CKB and rearrange these to form the orange parallelogram. Choose L to make LC = AK, and draw LM // CB.
You can demonstrate this P-slide in the adjacent figure using in turn: mouse enter, mouse click, double click, mouse exit. Try it!
Our second technique is the more difficult quadrilateral slide or Q-slide. This is a 4-piece dissection for transforming a quadrilateral into another quadrilateral having different side lengths but the same angles.
 Check out this figure at left. We are going to dissect the orange quadrilateral into the green quadrilateral. Point E is an obvious intersection point, F is chosen to make DF = KJ, G is the midpoint of AE, H is the midpoint of FC. The little added segment at F is parallel to the common base. The small triangles with opposite angles at common vertex G are congruent, as are the small triangles with opposite angles at H.
Check out this figure at left. We are going to dissect the orange quadrilateral into the green quadrilateral. Point E is an obvious intersection point, F is chosen to make DF = KJ, G is the midpoint of AE, H is the midpoint of FC. The little added segment at F is parallel to the common base. The small triangles with opposite angles at common vertex G are congruent, as are the small triangles with opposite angles at H.
You can demonstrate the Q-slide in this figure as we did for the P-slide. Try it!
There are some limitations to the application of the Q-slide, but it works in general. It is a little unsatisfactory from a practical point of view, as one needs to know the dimensions of the (green) image quadrilateral to set up the slide. This is not generally an easy task.