3. AREA

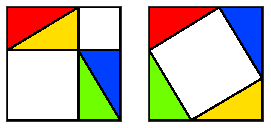
Consider the two large congruent squares at right. The left-hand square has been dissected into 4 triangles and 2 smaller squares. In the right-hand square, the triangles are rearranged leaving a large white ‘diagonal’ square. We claim that the sum of the areas of the two white squares at left equals the area of the white ‘diagonal’ square at right. We do this because it is intuitive that a dissected polygon is ‘the sum of its parts’. In other words, area is preserved when we carry out a dissection. Thus:

If a polygon (set of polygons) S is dissected and rearranged to give a polygon (set of polygons) T, then the area of S equals the area of T.

More interesting is the converse result which is in fact true, and easy to prove:

If polygons (sets of polygons) S and T have the same area, there exists a dissection of one to the other.



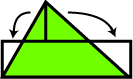
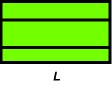
Proofs of Pythagoras’ theorem using dissections depend on the fact that areas remain the same.

We start with polygon S having area A, and dissect it into triangles. Each triangle can now be dissected into a rectangle as shown in the second figure. Next, since a rectangle is a special parallelogram, we can use a P-slide to dissect this rectangle into a rectangle of length L, for some chosen length L. Finally we stack all the rectangles of length L to form a rectangle R of height A/L.

Similarly we can begin with polygon T and dissect it into the same rectangle R. Hence S can be dissected into R which can then be dissected into T (reversing the second dissection). This completes our proof.

Of course this dissection is not at all economical; all we need here is its existence.