13. A CATALOGUE OF CHAOS

Julia sets, coordinate systems, more complex numbers

























  

Coordinate systems

In the last section, we considered complex numbers of the form x+iy, and we saw how such numbers could be interpreted as points in the complex plane. The real and imaginary components of the number correspond to the x– and y–coordinates of the associated point. Such x– and y–coordinates are called Cartesian coordinates. Each point in the plane is uniquely identified by its Cartesian coordinates.

Cartesian coordinates are not the only possibility. We can also use polar coordinates, (r,) to identify a point P. As shown in the diagram, r is the distance of P from the origin, and is the angle between the x–axis and the line OP. These two quantities also uniquely identify the point P, if P O.
It is possible to calculate each type of coordinates from the other, using the relationships:

x = r.cos
y = r.sin .

1. Work out formulae for calculating r and from x and y. (Take care with the formula for .)

If the point P represents a complex number z = x + iy, then the polar coordinates of P are called the modulus and the argument of z. We met the modulus in the last chapter in its usual notation of |z|. The argument is usually written arg(z).


























Complex geometry

The modulus and argument of a complex number have a simple geometrical interpretation. Can we find geometrical interpretations for other operations on complex numbers?

We earlier saw that the sum of two complex numbers z = x + iy and w = u + iv is:

z + w = (x + u) + i(y + v).

The geometrical interpretation of this is the well-known parallelogram law.
Interpretation of the product z.w is easier if we express z, w in terms of their polar coordinates. Suppose we have:
     z = r cos + ir sin
     w = s cos + ir cos

The product is then:
z.w = rs(cos + i sin )(cos + i sin )
= rs[(cos cos – sin sin )
     + i(sin cos + cos sin )]
= rs[cos( + ) + i sin( + )].

Thus to multiply two numbers, we multiply their moduli and add their arguments.

2. Choose a complex number z with a modulus just less than 1 and a small argument (say, r = 0.9 and = 10°). Plot it on a graph at a suitable scale. Then calculate and plot the positions of z2, z3, z4 and so on. (This is easiest in polar coordinates.) What shape do we get?

A sequence of powers of a complex number leads naturally to a spiral formation. It is no coincidence that spirals occur so often in the Mandelbrot set.

3. Show that the above formula for z.w in terms of polar coordinates is equivalent to the Cartesian form.

We now use these ideas to investigate a family of fractals that is closely related to the Mandelbrot set: the Julia sets.

























Julia sets (I)

Julia sets are generated by the same formula that gives us the Mandelbrot set:
           zn+1 = zn2 + c.

To get the Mandelbrot set, we always used z0=(0,0) and plotted the behaviour of the formula for each point c in the complex plane. To get the Julia set J(c), we choose a particular value for c, and plot the behaviour of the formula for each starting point z0 in the complex plane. There is a different Julia set for each choice of c. An example (J(-0.6+0.42i) is shown at right.

Strictly speaking, the Julia set comprises only the boundary of the black area in the picture. The picture shows a ‘filled in’ Julia set, whose structure is easier to see. As with the Mandelbrot set, we can draw coloured contours around the Julia set to make the image more spectacular. Our program will display Julia sets coloured in this way.

Some Julia sets are connected (all black areas are connected in one piece, as below; some are disconnected (with separate ‘islands’ of black). Can we tell from given complex number c, if J(c) is connected or not? The Mandelbrot set helps answer this question.






















Julia sets(II)

View the Julia sets:
J(-0.1+0.8i) (illustrated),
J(-0.6+0.42i), J(-0.75), J(-1), J(i).

4. Check the values of c associated with these Julia sets in an image of the Mandelbrot set. Are they in the Mandelbrot set or not? You may need to use a calculator to check. Do you think there might be a relationship between c being in the Mandelbrot set and J(c) being connected?

5. A small change in c can produce a big change in the appearance of J(c). In the group of images given above, for example, compare the sets J(0.25) and J(0.26). Use your program to explore the region between these values of c, to discover where and how this change occurs.

The following program is very similar to the previous one for the Mandelbrot set. Procedures while and dot, again used in this program, are not given here, but need to be included.


























The program
to Julia :cx :cy
seth 90 ht
make “y -80
repeat 161 [
make “x -100
repeat 201 [
setc JuliaColour :x 80 :y 80 :cx :cy
dot se :x :y make “x :x + 1]
make “y :y + 1]
end

to JuliaColour :x :y :cx :cy
make “a :x make “b :y make “n 0
while [and :a * :a + :b * :b < 4 :n < 16)] [
make “newb 2 * :a * :b + :cy
make “a :a * :a - :b * :b + :cx
make “b :newb make “n :n + 1]
if :n > 15 [make “n 0]
output :n
end
Julia -0.27 1.04


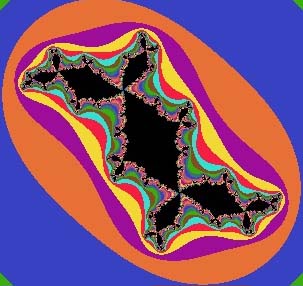
The program generates the illustrated Julia set, J(-0.27+1.04i). To obtain other Julia sets, allot different parameters in the last line.





















Julia sets and the Mandelbrot set

Since they have the same generating formula, it should not be surprising that there are many interesting relationships between Julia sets and the Mandelbrot set. The Mandelbrot set can be defined as the set of points in the complex plane for which the associated Julia set is connected. A further connection is more profound. The Mandelbrot set contains, in a sense, a copy of every Julia set. Given a particular complex value c, the Julia set J(c) around the point z = c, on magnification, yields essentially the same image as the Mandelbrot set magnified around point c.

6. Choose a magnified image of the Mandelbrot set, for which you know the coordinates of the centre, c. Generate the Julia set for this value of c. What characteristics do the two pictures have in common?
For example, the left picture shows a magnification of the Mandelbrot set around the point c = –0.724102 + 0.286462i. Note the 11-bladed ‘fan’ structure. The right picture is a magnification of the Julia set J(c) around the point z = c. Except for scaling and rotation, it looks the same as the first picture. This happens for every point on the boundary of the Mandelbrot set. The Mandelbrot set can be regarded as a catalogue of the Julia sets.






















Further investigations

7. The last two chapters have discussed complex multiplication, but not division. Let us work out a formula for the result of dividing one complex number by another, in terms of the components of the two original numbers. Let the two numbers be z = x + iy and w = u + iv. The expression for z/w is easily obtained:            

The problem is to separate the real and imaginary components of the expression. Start the process by multiplying both the numerator and denominator by u – iv. This number is called the complex conjugate of w.

8. (Harder) There are Julia Sets based on other functions besides z2+c. One class of attractive symmetrical Julia Sets is based on Newton’s method for solving equations.

See how the relationship:

zn+1 = zn – (zn4 – 1)/4zn3

behaves for different values of z0.

Because this relationship involves a complex division, you should try Investigation 7 first.