|
|
|
|
2. Length of a coastline 3. The Koch Island 4. The Logo program 5. Further investigation  |
 Simple perimeters Simple perimeters
It is very easy to calculate the perimeter of a polygon: we just take the lengths of sides of the polygon, and add them together. Thus in the diagram, the perimeter P(Q) of quadrilateral Q is P(Q) = AB + BC + CD + DA.
|
1. Draw a circle of radius 8 cm. Set your compass or dividers to a distance of 8 cm say. Starting at the point S, step off arcs around the circle, stopping before you reach S again. If the set distance is denoted by D, and the number of steps taken is N, then we can set up the first row of a table as follows.
Now repeat the procedure taking smaller and smaller values of D: 6, 4, 3, 2, 1, 0.5, 0.25, entering your values in the table. What do you notice about the entries in the final column? We observe that the entries approach more and more closely to the expected value of ‘2 |
||||||
| Length of a coastline
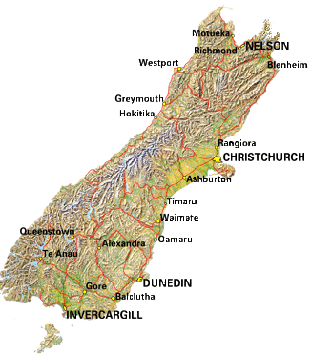
We now look at a more difficult case. Suppose we want to estimate the length of athe coastline of the South Island of New Zealand. 2. (a) Now with a measured length of 4 cm on your ruler, starting at Christchurch, step around the coastline on the screen, and calculate the approximate length as you did for the circle. Repeat with measured lengths of 3, 2, 1, 0.5, and enter your results in a table as before. What do you find? (b) Think about this situation. As you set your measured lengths smaller and smaller, you will finally (in theory!) be measuring around small stones, and then grains of sand! Do you think there will be a finite length for the coast line? |
 |
| The Koch Island
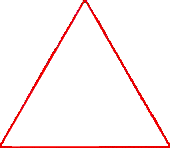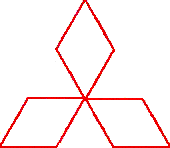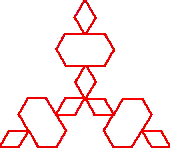
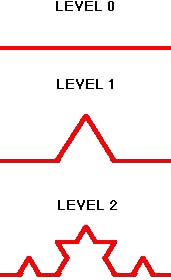
We now look at the coast length of a rather special island called the Koch Island. It is also known as the snowflake curve. It is based on an equilateral triangle, but we describe the construction on one side of the triangle; the other sides are treated similarly. We begin with a single line segment. We call this stage of the process level 0. We next divide the segment into thirds, and replace the middle third by the other two sides of an equilateral triangle, standing on this middle third as its base, and facing ‘outwards’. This is level 1 (see adjacent figure). The process is now repeated on each segment of the level 1 figure to obtain the level 2 figure. The process is continued for an infinite number of steps to obtain the Koch Island. We next give a simple Logo program which generates the Koch Island (well, at least an approximation to it!). |
 |
| The Logo program
In this program, KochIsland gives the triangular shape but replaces each triangle side with the shape generated by KSide. The procedure KSide simply instructs the turtle to draw the shape which we discussed above. It begins with a ‘cut-out’ statement (if :level = 0 ... ) to prevent the recursion continuing indefinitely. We can decide which level we want to generate by choosing the level number in the program. Here we have chosen the size to be 150 and the level number to be 4. |
|
||||||||||||||||||||||
| Further investigations
4. A Spanish encyclopedia claims that the border between Spain and Portugal has length 616 miles, while a Portuguese encyclopedia quotes 758 miles. How do you think such a difference could occur? 5. Devise your own experiment for calculating
|
 6. The gear wheels of a bicycle have radii 80 cm, 50 cm. If the smaller wheel has 21 teeth, how many teeth has the larger wheel? Is there arelationship between the diameters and the numbers of teeth on the gear wheels of your bicycle? 7. An interesting variation of the snowflake curve called the anti-snowflake curve can be constructed by placing the triangle constructions inwards rather than outwards. The resulting figure is then bounded by the original triangle. Modify the program to obtain this new fractal figure. |


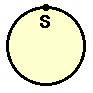 When it comes to calculating the perimeter (or circumference) of a circle, life is not so easy. However, it is easy to get an approximate value for the perimeter as follows.
When it comes to calculating the perimeter (or circumference) of a circle, life is not so easy. However, it is easy to get an approximate value for the perimeter as follows.