|
||
|
| Ten little piggies ...
We learn how to count from early childhood. And because most of us have ten fingers and ten toes, it is not surprising that the number 10 plays a key role in our counting system. Thus 6347 is our short-hand for
or 9 We say that our numbers are expressed in base 10, or decimal (from the Latin word decem for 10). You may have never appreciated how easy it is to calculate in the decimal system, but be thankful you weren't a tax collector in ancient Rome! Roman numbers were not written to any base. From 1 to 100 the Roman numbers were: |
1. (a) Express in Roman notation: (b) In the decimal system, work out (c) Work out some other products in the decimal and Roman systems. Clearly working with a base has some big advantages. But need we take base 10? |
|
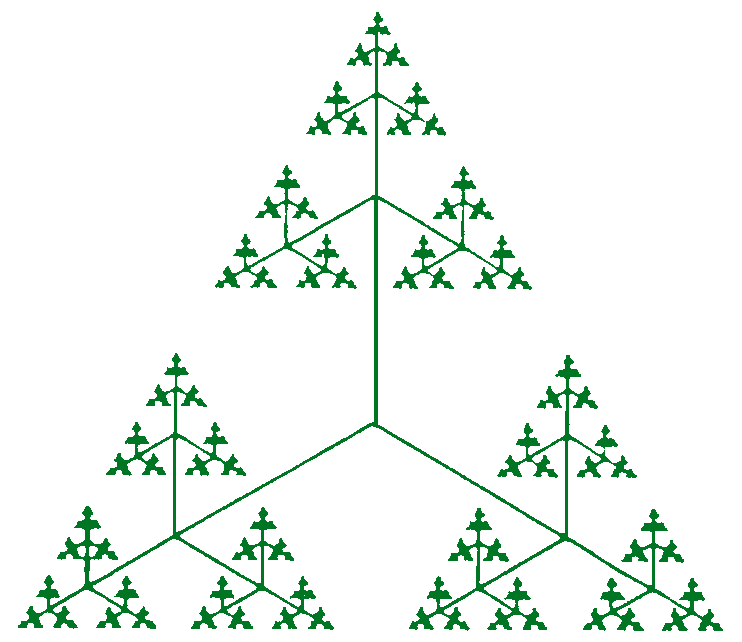
| The ternary tree
The fractal generated by this short program is made up of many ‘triads’ – groups of three segments radiating out from a common end-point at angles of 120°. The program is controlled by two inputs:
|
For the ternary tree in this figure,we have chosen a factor value of 0.5. |
||
| Counting in threes
We now look more closely at the first few levels of the ternary tree construction. In the diagram below, we have slightly separated the sets of newly added triads at each level. Suppose we want to label the segments at each level. 2. How many new segments are added each time? What is the obvious pattern?
|
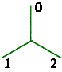 Level 1: we use 0 to denote the vertical segment, 1 the right segment, and 2 the left segment – i.e. number the segments clockwise from the top. Level 1: we use 0 to denote the vertical segment, 1 the right segment, and 2 the left segment – i.e. number the segments clockwise from the top.
Level 2: we denote each new segment by a two digit label: the first digit denotes the level 1
(b) Without drawing the level 4 fractal, describe the position of the segment with label 1202. |
|
Base 3 numbers
Although we have discounted labelling the new level 3 segments from 1 to 27 as being unhelpful, there is a relationship between this natural counting and our place labels with 0s, 1s and 2s. The place labels have a natural ordering:
000, 001, 002, 010, 011, 012, 020, 021, 022, Suppose now that beginning with 0 (to correspond to the label 000), we match these with the numbers 0 through to 26. Thus we would obtain the correspondence 000 We can transfer from one system to the other with relative ease. Thus, 122 |
Working in the other direction, we divide through repeatedly by 3:
17 = 3 We say that 122 is the base 3 (or ternary) representation of the number 17. 4. (a) Express 13, 19, 24 to base 3 (i.e., find the corresponding labels). Count off segments on the ternary tree to check your result. Now try 43, 55, 78. (b) What (base 10) numbers are represented by 021, 111, 210? Check your answers. Now try 2210, 1210, 1111. We can use any base b > 1, (b a positive integer). We know 10 is a popular choice for b. Also b = 2 is often used, particularly in computing; we then obtain the binary system. |
| Further investigations
5. Use your library to find out about the number systems used by the Egyptians, the Babylonians, the Greeks and the Mayans. The way our present day number system and numerals developed makes very interesting reading. 6. We have illustrated the ternary tree giving a value of 0.5 to the variable ‘factor’. Try running the program with different values of ‘factor’. What happens if the values are greater than 0.5? Can you explain why some choices of this variable give ternary trees of greater complexity (more levels)? 7. The ternary tree program is based on three segments meeting at a point. Investigate what happens when 4 or more equally spaced segments meet at a point. |
8. The digits used in the binary system are just 0 and 1. The numbers 0, 1, 2, ... are then expressed as 0, 1, 10, 11, 100, 101, 110, 111, 1000, ... . What is the binary expression for 17? 23? 45? 64? What is the decimal expression for the binary numbers 1111? 10000? 10101? Explain how it is possible to go from one system to the other.
9. In Section 5 we saw how the Sierpinski sieve can be constructed. |



 branch to which the segment is attached, the second its position in the smaller triad, using the same system as in level 1. Notice that the segment label gives complete information about the size and position of the segment.
branch to which the segment is attached, the second its position in the smaller triad, using the same system as in level 1. Notice that the segment label gives complete information about the size and position of the segment. 3. (a) Complete the labelling in these level 2, 3 fractals.
3. (a) Complete the labelling in these level 2, 3 fractals.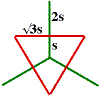 A delightful alternative construction can be carried out by adapting the Ternary Tree procedure: in place of each triad of segments, construct three sides of an equilateral triangle as in the figure. See if you can adapt the program in this way.
A delightful alternative construction can be carried out by adapting the Ternary Tree procedure: in place of each triad of segments, construct three sides of an equilateral triangle as in the figure. See if you can adapt the program in this way.