| Pythagoras’ theorem
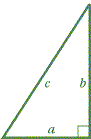
Probably the most famous of all the theorems left to us by the ancient Greeks is the theorem of Pythagoras. It concerns the areas of squares constructed on the three sides of a right-angled triangle. If AB2 = BC2 + CA2. We do not know how Pythagoras proved his result, but it is likely that he used a dissection method like that illustrated below. We let a, b, c denote the side-lengths of sides BC, CA, AB of &Mac198;ABC above. |
1. Noting that in the figure below the eight triangles are congruent (have the same size and shape), can you deduce Pythagoras’ theorem?
Incidentally we observe that for a right-angled triangle with sides of length a, b and hypotenuse (longest side) of length c, Pythagoras’ theorem can be simply expressed as a2 + b2 = c2. We shall come back to this expression a little later.
|
 The Pythagorean tree The Pythagorean tree
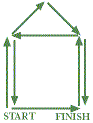
The Pythagorean tree is a fascinating fractal based on the Pythagoras construction. We give here the version where the right-angled triangle is isosceles. This gives rise to a symmetric tree. The Logo program corresponds to the illustrated drawing sequence. The roof of this ‘house’ is right-angled, and the tree construction is reproduced outwards from the sloping ‘roof’ arrows. |
|||
|
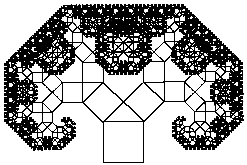
The resulting fractal is pictured below.
|
||
| Real or rational?
The real numbers are the labels we give to points on the real number line. Examples are –2, –2/3, 0, 1, 2. Let the large square in the Pythagorean tree have side-length 1. What is the size of the first few smaller squares, in decreasing order? Can you see a pattern? You should obtain a sequence which starts 1, 1/
|
3. (a) Suppose
(b) Show that a must be even. (What would happen if a were odd?) If a is even, we can write a = 2d. (c) Show that the equation a2 = 2b2 now becomes 4d2 = 2b2, i.e., 2d2 = b2. (d) Show that now b must be even. The Pythagoreans saw that if a and b are both even, then the common factor of 2 can be cancelled out. This gives a contradiction, as we have assumed that a and b have no such common factor. These days we argue that our original assumption must have been wrong, i.e., it is not true that |
|
Pythagorean triples
As we have seen, Pythagoras’ result can be written as a2 + b2 = c2. Of special interest is the case where a, b, and c are all integers. A simple example is 32 + 42 = 52. We say that (3, 4, 5) is a Pythagorean triple. Are there any others? In fact a general formula for Pythagorean triples has been known since the time of Diophantus and the early Greeks. |
4. (a) Let m, n be any positive integers. We set a = m2 – n2, b = 2mn, c = m2 + n2. Complete the table below.
(b) Can you show that if (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc), for any positive integer k? A little calculation gives: (m2 – n2)2 + (2mn)2 = (m2 + n2)2. It is known that the formulae in Question 4 give rise to all Pythagorean triples. |
||||||||||
| Further investigations
5. Use your library to discover more about Pythagoras. There are many interesting stories about him and his discoveries.
7. When the Egyptians built the pyramids, they may have used a loop of rope on which there were 12 equally spaced knots to ensure that the blocks were placed ‘on the square’. Explain how they would have used this rope. |
8. It is possible to use the method of Q 3 to show that
9. Look back at your table of Pythagorean triples. Notice that for (3, 4, 5) and (5, 12, 13) the last two integers are just 1 apart. Notice how m and n are related here. Can you find other Pythagorean triples in which the last two integers differ by 1?
|


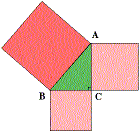

 The discovery of
The discovery of 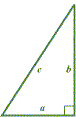
 6. Pythagoras’ theorem for an isosceles right-angled triangle is often seen illustrated in floor mosaics. See if you can find examples of this.
6. Pythagoras’ theorem for an isosceles right-angled triangle is often seen illustrated in floor mosaics. See if you can find examples of this.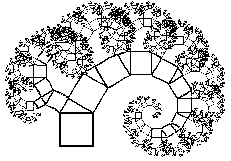 10. We constructed the Pythagorean tree based on an isosceles right-angled triangle. If we choose a non-isosceles triangle, we obtain a lop-sided Pythagorean tree. See if you can modify the program to generate such a tree.
10. We constructed the Pythagorean tree based on an isosceles right-angled triangle. If we choose a non-isosceles triangle, we obtain a lop-sided Pythagorean tree. See if you can modify the program to generate such a tree.