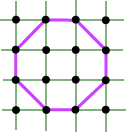
|
4. CONVEX LATTICE POLYGONS I had been looking at my lecture notes on Pick’s Theorem, when the thought suddenly came to me. Suppose you have a lattice polygon P with a fixed number I of interior points, and you insist that it be convex. Now try to increase the number of boundary points B, while keeping I fixed, and retaining the convexity. Might we not expect there to be some bound on the number B? It turns out that there are two cases to consider: (a) convex lattice polygons with I = 0 Suppose we look at Case (a). We quickly find the set of polygons:
for which I = 0, and B = 4, 6, 8, ... . This means that for I = 0, the number of boundary points B can be made arbitrarily large. Thus there is no upper bound on B.
|
|||||||||||||||||||||||||||||
 |
 |
 |
|||||||||||||||||||||||||||
1.
|
Answering the above question, you should have found convex lattice polygons with the following values of B, I.
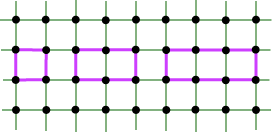
The pairs at right come from a sequence of rectangles of width 2, like the first two polygons below.
In this sequence, there seem to be six end boundary points, and each interior point is associated with two further boundary points. This suggests B = 2I + 6, and we might have conjectured B Convexity Theorem. If P is a convex lattice polygon with B boundary points and I interior points, then We observe that this result will remain true for any planar lattice, since it just depends on the numbers B and I. This result was first discovered by Scott [S]. I find it amazing that this simple result could have remained undiscovered for so long. We won’t give the whole proof here, but we can make some observations. Suppose we set g(P) = B – 2I (remember how we handled Pick’s Theorem). The statements of the Convexity Theorem now become: g(P) 1/2 g(P) = B – A – 1 = A – 2I + 1.
Then A(P) It follows that g(P) • p = 2, or h + k • p = 3 and h + k • p We see that in order to establish our theorem, we now only need consider lattice polygons which do not satisfy these conditions. For details of the completion of the proof, see [S]. Various other results are known or conjectured when some restriction is placed on the size or shape of the lattice polygon. (1) For example, suppose P is a convex lattice pentagon. What is the smallest number of interior points it can have? Try some examples! Eugene Ehrhart [E] gives the answer to this (in French!). Check. In fact, it is relatively easy to obtain a sequence of results of the form: A convex lattice n-gon contains at least I(n) interior points. (2) In 1978, Coleman [C] independently proved the Convexity Theorem. For convex polygons with I > 0, he proposed the relatively weak inequality B He then makes the interesting conjecture: If a convex lattice polygon has n sides, then B Coleman also establishes a result in the other direction for convex lattice n-gons: I The proof is rather involved, but we can easily check the first part. For n = 3 or 4, [(n – 3)/2] = 0, and clearly I (3) John Arkinstall [A] incorporated Ehrhart’s result and extended it as follows. For a convex lattice n-gon P: • n = 4 and P has no pair of parallel edges Stanley Rabinowitz [R] later used some computer help to list all convex lattice polygons in the plane (up to equivalence) with at most one interior lattice point. (4) We can improve the Convexity Theorem inequality if we add further constraints to the lattice polygon. For example suppose we insist that all the angles in the polygon P be acute. Then B Of more interest is when we insist that every angle of P be obtuse. What do you think the inequality might be in this case? Find an example where equality holds. Check. (5) Jamie Simpson [Si] suggests looking for convex lattice n-gons which have minimal area for given n. He shows that for n a(n) = g(n) + n/2 – 1, where a(n) denotes the minimal area, and g(n) the minimal number of interior points for the given value of n. He gives values of a(2n) for low values of n. (6) Ross Honsberger [H] observes that an n x n square S can be placed in the plane with its sides parallel to the coordinate axes to cover (n + 1)2 lattice points. He then asks if S can ever cover a greater number of lattice points if it is just tossed onto the lattice plane. For the answer, see Honsberger [H]. [A] Arkinstall, J. R., Minimal requirements for Minkowski’s Theorem in the plane, Bulletin of the Australian Mathematics Society 22 (1980) 259 – 274. [C] Coleman, D. B., Stretch: A geoboard game, Mathematics Magazine 51 (1978) 49 – 54. [E] Ehrhart, E., ‘Propriétés Arithmogeometriques des Polygones’, Comptes Rendus 241 (1955) 686–689. [H] Honsberger, R., ‘A square in a lattice’, Mathematical Morsels, Dolciani Mathematical Expositions No. 3, Mathematical Association of America (1978). [R] Rabinowitz, S., A census of convex lattice polygons with at most one interior lattice point, Ars Combinatoria 28 (1989) 83 – 96. [S] Scott, P. R., On convex lattice polygons, Bulletin of the Australian Mathematical Society, Number 3, Volume 15 (1976) 759 – 767. [S2] Scott, P. R., An inequality for convex lattice polygons, Mathematics Magazine, 52 (1979) 239 – 240. [Si] Simpson, R. J., Convex lattice polygons of minimum area, Bulletin of the Australian Mathematical Society Volume 29 (1990) 353 – 367.
|
||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
2I + 6, were it not for the surprise triangle at right. Did you find it? So, our conjecture becomes B 
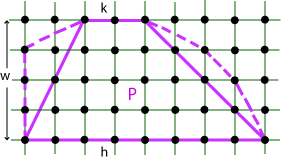Now, how would we begin to prove the Convexity Theorem? Suppose our (convex) polygon P contains this lattice trapezium with parallel sides of length h and k placed distance w apart.
I 
