|
3. AREA OF LATTICE POLYGONS
|
|||||||||||||||||||||||||||||||||||||||||||
|
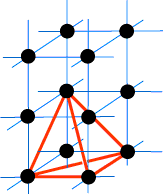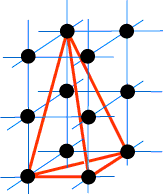
Our experimentation leads us to conjecture the result known as: Pick’s Theorem: Suppose a simple lattice polygon P has area A, B boundary points and I interior points, then f(P) = A – B/2 – I + 1. We call this Pick’s formula. Then f(P) = 0 becomes the statement of Pick’s Theorem. (1) We first show that Pick’s formula is additive. This means that if we adjoin two lattice polygons for which Pick’s formula is true to obtain a new lattice polygon P, then the formula for the new polygon P will be given by the sum of the formulae for the two contributing polygons. This will become clearer shortly. (2) Since every lattice polygon P can be constructed by assembling together lattice triangles, Pick’s formula for P will be the sum of Pick’s formulae for all the contributing triangles. If we can show that for any such triangle T, f(T) = 0, Pick’s Theorem will follow. (1) Let us begin at the beginning! Look at this example:
Here we are combining two lattice polygons P1 and P2 to obtain a new lattice polygon P (or P1 + P2).
Notice from the figure that we have added the areas, lost 1 boundary point (twice) and gained one interior point. The B column in the table appears inconsistent with this because we have also counted the two endpoints of the common segment twice. Let’s try to work this through in general. Let P1 have attributes A1, B1 and I1 (in the obvious notation) and P2 have A2, B2 and I2. Suppose the boundary which is in common contains k lattice points. We now obtain:
Now, let’s check the final entry in the table. Using the values of A, B and I for P, we obtain: f(P) = A – (B1 + B2 – 2k + 2)/2 – (I1 + I2 + k – 2) + 1 = (A1 – B1/2 – I1 + 1) + (A2 – B2/2 – I2 + 1) We say that the formula f is additive for polygons related in this way. Obviously if we wrote P1 = P – P2, the formula also remains true under subtraction.
We observe that any lattice triangle can be placed inside a lattice rectangle with sides parallel to the coordinate axes.
There are a number of different cases to consider here, but they all involve lattice rectangles (such as R) and right-angled lattice triangles (such as P) with sides parallel to the coordinate axes. We check Pick’s Theorem for these rectangles and triangles. Rectangle Case: Suppose the rectangle U (for example) has length l and width w. Triangle Case: Consider now the triangle P (for example) with side lengths l and w, and by assumption, no points on the hypotenuse. Conclusion: We illustrate the final argument using the most difficult third case above. By Part (1) of our proof f(U) = f(P) + f(Q) + f(R) + f(S) + f(T) This completes the proof of Pick’s Theorem. A shorter but more sophisticated proof of the second part of our proof is given in Coxeter [C]. Some proofs involve showing that the area of the primitive triangle defined earlier (a lattice triangle with B = 3 and I = 0) is 1/2. (See Chapter 2.) Further results (1) An obvious question to ask is whether an analogue of Pick’s Theorem holds in 3-space. Experiment with a few very simple lattice polyhedra (for example, tetrahedra). In 1957, Reeve [R] obtained a result in 3-space with the ingenious idea of introducing a secondary lattice – in fact the lattice of all integer multiples of (1/2, 1/2, 1/2). MacDonald [M] later extended this to higher dimensions. It is a nice idea, but the results lack the appealing simplicity of Pick’s Theorem. There is an analogue in this case. It can be shown that A = B/2 + I + k, where k is a number involving the Euler characteristic of the region and the boundary. If you are interested in following this up, see Scott [S]. However, we shall be looking at this further in Chapter 6, where we investigate the link between Pick’s Theorem and Euler’s Formula. (3) A third question to ask is whether Pick’s Theorem continues to hold for a more general planar lattice. (5) What do lattice triangles look like? Reznick [Re] looks at lattice simplices in En with B = n + 1 and I = m. He classifies such lattice triangles for n = 2, and shows that if m = 1, the interior lattice point is the centroid (centre of gravity). [C] Coxeter, H.S.M., Introduction to Geometry, (Wiley) (Edition 2 1969) [DKR] Ding, R., Kolodziejczyk, K., Reay, J., A ne Pick-type theorem on the hexagonal lattice, Discrete Mathematics 68 (1988) 171 – 177. [GKW] Gaskell, R. W., Klamkin, M. S., Watson, P., Triangulations and Pick’s theorem, Mathematics Magazine, 49 (1976) 35 – 37. [H] Haigh, G., A natural approach to Pick’s Theorem, Mathematical Gazette 64 (1980) 173 – 177. [L] LattE Background http://www.math.ucdavis.edu/%7elatte/latex/pick/pick/ [M] MacDonald, I. G., The volume of a lattice polyhedron, Proceedings of the Cambridge Philosophical Society 59 (1963) 719 – 726. [P] Pick, Georg, Geometrisches zur Zahlenlehre, Sitzungsber Lotus Prag 19 (1900) 311 – 319. [R] Reeve, J. E., On the volume of lattice polyhedra, Proceedings of the London Mathematical Society (3) 7 (1957) 378 – 395. [Ra] A census of convex lattice polygons with at most one interior lattice point, Ars Combinatoria 28 (1989) 83 – 96. [Re] Reznick, B., Lattice point simplices, Discrete Mathematics 60 (1986) 219 – 242. [RKMR] Ren, D., Kolodziejczyk, K., Murphy, G. and Reay, J, A fast Pick-type approximation for areas of H-polygons, American Mathematical Monthly 100 (1993) 669 – 673. [S] Scott, Paul R, The fascination of the elementary, Hanna Neumann Lectures at ICME V, (Ed) Newman, M.F. (1986) 75 – 88; Amer. Math. Monthly 94 (1987) 759 – 768. [V] Varberg, D. E., Pick’s Theorem revisited, American Mathematical Monthly 29 (1985) 584 – 587. [W] Wikipedia Answers.com, http://www.answers.com/topic/pick-s-theore |
||||||||||||||||||||||||||||||||||||||||||
 It is clear that lattice polygons come in various shapes and sizes. A very small lattice triangle may cover just 3 lattice points – at the vertices. A very large lattice polygon might be expected to cover many more lattice points. This suggests that there might be a correlation between the area of (simple) lattice polygons and the number of lattice points they cover. Let’s see if we can find a formula. We let A stand for the area, B for the number of boundary points, and I for the number of interior points.
It is clear that lattice polygons come in various shapes and sizes. A very small lattice triangle may cover just 3 lattice points – at the vertices. A very large lattice polygon might be expected to cover many more lattice points. This suggests that there might be a correlation between the area of (simple) lattice polygons and the number of lattice points they cover. Let’s see if we can find a formula. We let A stand for the area, B for the number of boundary points, and I for the number of interior points.

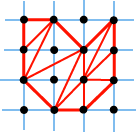 (2) We now assert that any lattice polygon can be subdivided into lattice triangles, and in fact lattice triangles with boundary lattice points only at the vertices, i.e. with B = 3. Try some examples: you will be easily convinced. So by Part 1, we only need to show that Pick’s Theorem is valid for these triangles.
(2) We now assert that any lattice polygon can be subdivided into lattice triangles, and in fact lattice triangles with boundary lattice points only at the vertices, i.e. with B = 3. Try some examples: you will be easily convinced. So by Part 1, we only need to show that Pick’s Theorem is valid for these triangles.