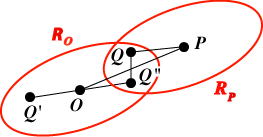
Let L denote the integer lattice. Minkowski’s Theorem Let R be a convex region with area A, which is symmetric about O. It is sometimes useful to restate this last sentence in its equivalent contrapositive form: Then R contains no points of L other than O implies that A Proof of Minkowski’s Theorem Let R be symmetric about O and assume A(R) > 4. Let RO be the set obtained by contracting R about O using a scale factor 1/2. The A(RO ) > 1. Hence by the Non-Overlap Theorem, two of the regions RP of that theorem overlap. Hence there is a lattice point P such that RO and RP overlap. Let Q be some point in that overlap. Let Q' be the fourth vertex in the parallelogram OPQQ'. Then Q' belongs to RO since Q' is to O in RO as Q is to P in the congruent set RP. Let Q" be the reflection of Q' in O. Since RO is symmetric, Q" belongs to RO. Finally, the midpoint of QQ" lies in RO since RO is convex. But this midpoint is also the midpoint of OP. We conclude that the lattice point P lies in the original larger region R. Hence R contains a lattice point other than O, and the theorem is proved. Hardy and Wright [HW] give an alternative proof of this theorem. Further results (1) Minkowski’s Theorem is easily generalized to higher dimensions: the inequality for A becomes A > 8 in three dimensions, and more generally, in n dimensions, A > 2 n. The theorem also holds for a general lattice L, with the inequality becoming A > 4d(L), A > 8d(L), or A > 2 nd(L) respectively, where d(L) is the lattice determinant. (2) There are various ways of generalizing Minkowski’s Theorem. For example Sawyer [Sa] obtains a result for planar convex sets with a measure of asymmetry. Scott [S1] obtains an analogue for planar convex sets which are not necessarily symmetric, but satisfy a certain boundedness condition. If in E2 we constrain the boundary of our convex symmetric set to have a built in degree of curvature, then Melzac [Me] shows that the upper bound on the area A can be reduced from 4. (3) A rather simpler result is the observation by Scott [S2] that Minkowski’s Theorem continues to hold for a convex planar set which has a chord through the origin which has midpoint at O (that is, is symmetric in O), and which partitions the set into two regions of equal area. This is generalized to 3 dimensions in Scott [S3]. A further curious result in the plane concerns convex sets which are partitioned by the axes into four regions of equal area [S4]. (4) Essentially, Minkowski’s Theorem can be generalized by modifying (a) the convexity condition, (b) the symmetry condition, or (c) the lattice point condition. Scott [S5] gives an overview of these possibilities, together with an extensive bibliography. (5) George Szekeres [Sz] finds an inequality in the opposite direction. Let P be a parallelogram (in the plane) with O at its centre, but containing no other lattice points. If the side directions are specified, then the maximal value of the area of P satisfies: max A(P) > 2(1 + 1/ (6) Joseph Hammer [H1] shows that if K is a planar set, centrally symmetric about O, and with A(K) > [E] Ennola, V., On the lattice constant of a symmetric convex domain, Journal of the London Mathematical Society, 36 (1961) 135 – 138. [H1] Hammer, J., On some analogues to a theorem of Blichfeldt in the Geometry of Numbers, American Mathematical Monthly 75 (1968) 157 – 160. [H2] Hammer, J., Some relatives of Minkowski’s Theorem for 2 dimensional lattices, American Mathematical Monthly 73 (1966) 744 – 746. [HW] Hardy, G.H., Wright, E. M., An introduction to the theory of numbers, Oxford (Edition 4 1960), page 33. [Me] Melzac, Z. A., Minkowski’s theorem with curvature limitations, Canadian Mathematical Bulletin 2 (1959) 151 – 158. [M] Minkowski, H., Geometrie der Zahlen, Leipzig and Berlin, 1896. [Sa] Sawyer, D. B., The lattice determinant of asymmetrical convex regions (II), Proceedings of the London Mathematical Society 3 (1955), 197 – 218. [Sa2] Sawyer, D. B., Lattice points in rotated convex sets, Quarterly Journal of Mathematics Oxford 13 (1962), 221 – 228. [S1] Scott, P. R., An analogue of Minkowski’s theorem in the plane, Journal of the London Mathematical Society (2) 8 (1974) 647 – 651. [S2] Scott, P. R., On Minkowski’s theorem, Mathematics Magazine 47 (5) (1974) 277. [S3] Scott, P. R., Convex bodies and lattice points, Mathematics Magazine 48 (2) (1975) 110 – 112. [S4] Scott, P. R., A new extension of Minkowski’s theorem, Bulletin of the Australian Mathematical Society 18 (3) (1978) 403 – 406. [S5] Scott, P. R., Modifying Minkowski’s theorem, Journal of Number Theory, 29 (1988) 13 – 20. [Sz] Szekeres, G., On a problem of the lattice plane, Journal of the London Mathematical Society 12 (1937) 88 – 93. [Sz2] Szekeres, G., Note on lattice points within a parallelopiped, Journal of the London Mathematical Society 12 (1937) 36 – 39. |
|||
 any lattice points’. Look at these sets:
any lattice points’. Look at these sets: 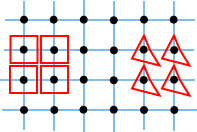 Looking at the squares at right, the result seems obvious, and you might rightly see this as an extension of the fundamental parallelogram idea for the lattice.
Looking at the squares at right, the result seems obvious, and you might rightly see this as an extension of the fundamental parallelogram idea for the lattice.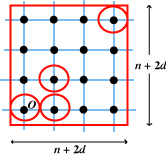 Proof of Theorem Let A denote the area of RO and let d denote the furthest distance of a boundary point of RO from O. Consider an n x n square of lattice points with their surrounding regions. These all lie inside an (n + 2d) x (n + 2d) square. We deduce that since the regions do not overlap, the total area of the regions is not greater than the area of this enclosing square. Hence
Proof of Theorem Let A denote the area of RO and let d denote the furthest distance of a boundary point of RO from O. Consider an n x n square of lattice points with their surrounding regions. These all lie inside an (n + 2d) x (n + 2d) square. We deduce that since the regions do not overlap, the total area of the regions is not greater than the area of this enclosing square. Hence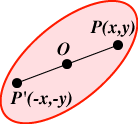 We next introduce the idea of symmetry.
We next introduce the idea of symmetry.