|
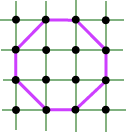
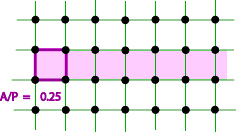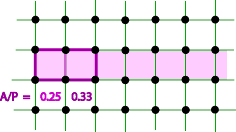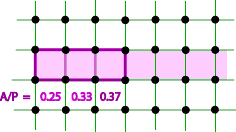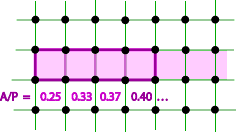
Hopefully you found that A(K) < 1/2P(K), equality being approached by long rectangles of unit width.
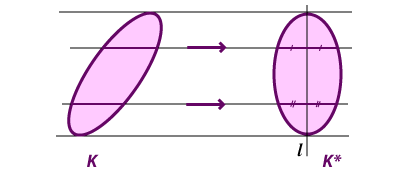
Notice the strange non-homogeneous nature of this inequality. If we enlarge K by a factor of s, then the left hand side is enlarged by factor s2, but the linear term on the right is scaled only by the factor s. This means that the inequality controls the size of K: if K gets too large, the inequality must fail. This fits with our idea of lattice-constrained sets: the sets are not able to increase in size indefinitely. Edward Bender [B] established this result in 1962. In retrospect, it is probably not an especially significant result within the subject, but it was significant for me, because it opened up the whole idea of non-homogeneous inequalities for lattice constrained sets. The proof also illustrates some useful techniques. So we have: Bender’s Theorem Let K be a convex planar set which contains no points of the integer lattice. Then A(K) < 1/2 P(K), and this inequality is best possible. Before we give the proof of Bender’s result, we outline a useful technique used in the proof. Steiner Symmetrization Let K be a convex planar set, and l a line in the plane. We obtain the symmetral K* of K with respect to l by translating every chord of K which is perpendicular to l so that its midpoint lies on l.
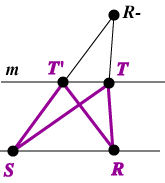
This gives us a new set, K*, which is (line) symmetric about the line L. We are now able to compare some of the properties of K and K*. (1) Like K, the symmetral K* is convex. Take any two points A' and B' in K*. These arise from points A, B in K as shown. Since K is convex, chord AB is contained in K. In fact, it is contained in the trapezium PQRS. It is now visually clear (and can be rigorously argued) that chord A'B' lies within the image trapezium P'Q'R'S' and so in K*. (2) A(K*) = A(K). Consider the contribution to the area made by corresponding thin strips of K and K*. Each strip is approximately a trapezium with parallel sides of length h and k and width w. Hence the area contribution of each is the same: 1/2 (h + k)w. Taking the limit as the number of equal width strips tends to infinity gives the result.
ST' + T'R = ST' + T'R– noting that the shortest distance from S to R– is a straight line. Summing the perimeter increments, we deduce that P(K*) Proof of Bender’s Theorem Let K be a convex planar set containing no points of the integer lattice. Symmetrize K about the line l having equation x = 1/2 to obtain a new set K*. From the properties of symmetrization above, K* is convex, A(K*) = A(K), and P(K*) We claim that K* contains no lattice points. For if K* contained a lattice point on the line y = k say (perpendicular to k), then since K* is symmetric, it must contain two lattice points on this line, and so a line segment of length Now A(K)/P(K) Suppose now that K is contained in the rectangle {(x, y) | 1/2 – a < x < 1/2 + a ; 1/2 – b < y < 1/2 + b }, where a, b are as small as possible. We may suppose that a
4 [This is a best possible result, with equality for a circle. A nice elementary ‘proof’ by Steiner is given in [YB], but this ‘proof’ assumes that an upper bound for A/P2 exists, and so is incomplete.] Now,
Finally, P(K) Bender published his area - perimeter result in 1962, but in fact it was known well before that. In 1948 the woman mathematician M. Nosarzewska [N] showed that if Z denotes the number of interior lattice points in a planar convex set, then A + 1/2P + 1 If the number of lattice points Z = 0, then the right hand side of this expression gives Bender’s inequality. Mathematical results are often proved independently. Remembering that Bender’s inequality has the (infinite) strip for its extremal strip, we might ask whether it can be extended to higher dimensions. Suppose we let V denote the volume and S the surface area of an n-dimensional convex set. Then in 1970 Hadwiger [H1], in 1972 Schmidt [Sc] and in 1974 Bokowski and Wills [BW1] showed that for n = 3, Z > V – 1/2F. For Z = 0 we obtain a direct analogue of Bender’s result, with an extremal set being the infinite slab of unit thickness. The inequality was extended to n-dimensions in 1972 by Hadwider, Bokowski and Wills [HBW]. Working in the other direction, Bokowski and Wills [BW2] in 1974, hinted at, and Overhagen [O] in 1979 showed that a convex set K in E3 satisfies Z where M is described as ‘the integral of the average curvature’ of K. An elegant but non-elementary conjecture of Wills extending the above inequality to general dimension has led to work by Hadwiger [H2], Hohne [Ho] and others. Further Results We now ask if there are any other inequalities relating the set parameters where the given convex set contains no points of the integer lattice. (1) Inequalities with one parameter. Clearly we will be looking for upper bounds. The infinite strip example shows that we should expect no upper bounds for the area A, perimeter P, diameter d or circumradius R. For the inradius r there is a trivial upper bound r
Check your answer. This pretty result is outlined in Scott [S]. (2) Inequalities with two parameters. We have already seen one of these with Bender’s Theorem. We might expect similar results relating A and d, or possibly A and R. Scott [S2] shows that A
The following table lists the current knowledge about the two-parameter inequalities. These results, and further details can be found in [HS1]. The table is symmetric about the lead diagonal: for example the A – p entry and the p – A entry give different information about the same topic. (3) Extensions to other lattices. Many of the above inequalities depend on the rectangular structure of the integer lattice, although (w – 1)(d – 1) (4) Extensions to higher dimensions. Bender’s area - perimeter inequality has been extended to higher dimensions by Joseph Hammer [Ha], Murray Silver [Si] and Jörg Wills [W]. (5) A further result. There are parameters that can be associated with K apart from the six defined above. For example, we can define the axial diameters, Xi(K) of K to be the segments of K of maximal length which are parallel to the axes. Then in n dimensions, if K contains no points of the integer lattice, the following pretty result is known [S7]:
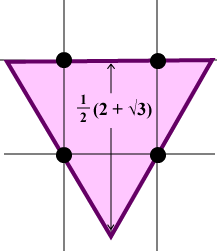
You will notice that in structure, this is closely related to the inequality (w – 1)(d – 1) (5) Sets with restrictions. Sallee [Sa] asks for the planar set of maximal constant width which can be placed to contain no points of the integer lattice. He shows that the extremal set is a Reuleaux triangle of width [A] Awyong, P. W., An inequality relating the circumradius and diameter of two-dimensional lattice-point-free convex bodies, American Mathematical Monthly 106 (3) (1999) 252 – 255. [AS] Awyong, P. W., Scott, P.R., New inequalities for planar convex sets with lattice point constraints, Bulletin of the Australian Mathematical Society 54 (1996) 391 – 396. [B] [B2] Bender, E., Area-perimeter relations for two-dimensional lattices, American Mathematical Monthly 69 (1962) 742 – 744. [BW] Bokowski, J., Wills, J., Eine Ungleichung zwischen Volumen, Oberfläche und Gitterpunktzahl, Acta Mathematica Academiae Scientiarum Hungarica 25 (1974) 7 – 13. [BW2] Bokowski, J., Wills, J., Upper bounds for the number of lattice points of convex bodies, American Mathematical Monthly 81 (1974) 620 – 622. [Ha[ Hammer, J., On a general area-perimeter relation for two-dimensional lattices, American Mathematical Monthly 81 (8) (1974) 884 – 885. [H1] Hadwiger, H., Volumen und Oberfläche eines Einkorpers, Mathematische Zeitschrift 116 (1970) 191 – 196. [H2] Hadwiger, H., Gitterpunktanzahl im Simplex und Will’sche Vermutung, Mathematische Annalen 239 (1978) 271 – 288. [HBW] Hadwiger, H., Bokowski, J., Wills, J., Eine Ungleichung zwischen Volumen, Oberfläche, und Gitterpunktzahl, Mathematische Zeitschrift 127 (1972) 363 – 364. [Ho] Hohne, R., Zur Gitterpunktanzahl im Simplex, Mathematische Annalen 251 (1980) 269 – 276. [HS1] [HS] Hillcock, P. W., Scott, P. R., Inequalities for lattice constrained planar convex sets, Journal of Inequalities in Pure and Applied Mathematics 3 (2) (2002) Article 23. [N] Nosarzewska, M., Evaluation de la difference entre l’aire d’une region plane convexe et la nombre des points aux coordonnees entiers, Colloquium Mathematicum 1 (1948) 305 – 311. [O] Overhagen, T., Zur Gitterpunktzahl konvexer Körper in 3 Dim Euklidischen Raum, Mathematische Annalen 216 (1975) 217 – 224. [Sa] Sallee, G. T., The maximal set of constant width in a lattice, Pacific Journal of Mathematics 28 (1969) 669 – 674. [Sc] Schmidt, W. M., Volume, Surface area and the number of lattice points covered by a convex set, Archiv der Mathematik, 23 (1972) 537 – 543. [S] Scott, P. R., A lattice problem in the plane, Mathematika 20 (1973) 247 – 252. [S2] [S22] Scott, P. R., Area-diameter relations for two-dimensional lattices, Mathematics Magazine 47 (4) (1974) 218 – 221. [S3] [S32] Scott, P. R., Two inequalities for convex sets with lattice constraints in the plane, The Bulletin of the London Mathematical Society 11 (1979) 273 – 278. [S4] Scott, P. R., Further inequalities for convex sets with lattice point constraints in the plane, Bulletin of the Australian Mathematical Society 21 (1) (1980) 7 – 12. [S5] Scott, P. R., Area, width and diameter of planar sets with lattice point constraints, Indian Journal of Pure and Applied Mathematics, 14 (4) (1983) 444 – 448. [S6] Scott, P. R., Convex sets and the hexagonal lattice, Mathematics Magazine, 51 (4) 1978 237 – 238. [S7] Scott, P. R., Lattices and convex sets in space, Quarterly Journal of Mathematics Oxford, 36 (2) 1985 359 – 362. [S8] Scott, P. R., On the volume and projection of convex sets containing no lattice points, Bulletin of the Australian Mathematical Society 32 (3) (1985) 331 – 338. [SA] Scott, P. R., Awyong, P. W., Inradius and circumradius for planar convex bodies containing no lattice points Bulletin of the Australian Mathematical Society 59 (1999) 163 – 168. [Si] Silver, M., Bender’s theorem and associated extremal figures, American Mathematical Monthly 81 (1974) 382 – 383. [W] Wills, J., On lattice points and the volume/area ratio of convex bodies, American Mathematical Monthly 78 (1971) 47 – 49. [YB] Yaglom, I. M., Boltyanskii, V. G., Convex Figures, Holt, Rinehart and Winston (1961). |
|||

 (3) P(K*)
(3) P(K*)  Case 1. a
Case 1. a  Case 2. a > 3/2. We consider K', the quarter of K with x
Case 2. a > 3/2. We consider K', the quarter of K with x  Inequalities not involving A are going to be more complex, as they need to be non-homogeneous. I was delighted to discover
Inequalities not involving A are going to be more complex, as they need to be non-homogeneous. I was delighted to discover