10. SETS CONTAINING LATTICE POINTS

We have been looking at inequalities between the parameters associated with convex sets which contain no lattice points. A natural extension of this is to ask about convex sets which contain a given positive number of lattice points.

We have already seen a couple of examples of this type involving just one interior lattice point:

Minkowski’s inequality [M], A 4 for sets symmetric about the origin, and

Ehrhart’s inequality [E], A 41/2 for sets with centre of gravity at the origin.

Neither of these is completely general, as each imposes an extra constraint on the convex sets K being considered.

Unfortunately, once we get beyond a single lattice point, complications set in, as even two lattice points can occur in different configurations. Hence there are two main types of problem discussed here:

• Parameter inequalities for sets containing exactly one interior lattice point.

• Parameter inequalities for sets containing a general number, n, of lattice points.

We wouldn’t expect upper bounds for the perimeter, diameter, or circumradius of sets containing just one lattice point (why?). Further the upper bound for the inradius is trivial.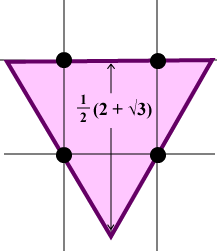

However, one of the nice inequalities for sets containing no lattice points occurs for the set of maximal width. Here we obtained w 1/2 (2 + 3), with equality for the illustrated triangle. An obvious question to ask is:

What is the maximal width of convex planar sets which contain just one interior lattice point?

Now check your answer.
              


































10. SETS CONTAINING LATTICE POINTS

I wonder if you found one of the following sets?

The equilateral triangle on the left is the most obvious choice. This set has w = (3 + 3)/2 2.36. I spent several weeks, on and off, trying to establish that this is the upper bound for the width. I then discovered, to my great surprise, the isosceles triangle on the right for which w = 1 + 2 2.41, and after some effort managed to show that 1 + 2 is the required upper bound. The proof can be found in [S]. There is a moral for researchers here: never assume that you know the right answer!

Further results

(1) Let us start with lattice point constrained sets containing just one lattice point. Quite a number of results are known here, but there are also many gaps in our knowledge. The table below contains most of the known results – and also quite a few question marks!

 
A
p
d
w
R
r
  
A
  
p
 
d
? 
 
w
?
 
 Extremal figure and inequality
R
? 
?
 
r
?
?


(2) Obvious questions to ask are whether any of the above results can be generalized for other lattices, and also whether any can be extended to higher dimension. Little is known here.

(3) A different idea is to seek results which apply to sets containing a general number, n, of lattice points. Such results naturally tend to be more complicated. Examples can be found in [S2], [S3], [S4] and [S5]. Elkington and Hammer [EH] give bounds for the number of lattice points contained in planar sets of given width. Working in Ed, Hammer [H] notes Hadwiger’s condition V > 1/2S for a set to contain at least one interior lattice point, and obtains V r/2.S as a condition for the set to contain at least r interior lattice points.

(4) Schaeffer [Sch] considered the problem of finding the planar convex set of least area which covers at least one point of the integer lattice in any position. He shows that a unit square with a pair of rounded opposite edges gives the best result. Vassallo [V] solves the corresponding width problem.

References

[AS1] Awyong, P. W., Scott, P. R., On the maximal circumradius of a planar convex set containing one lattice point, Bulletin of the Australian Mathematical Society 52 (1995) 137 – 151.

[AS2] Awyong, P. W., Scott, P. R., New inequalities for planar convex sets with lattice point constraints, Bulletin of the Australian Mathematical Society 54 (1996) 391 – 396.

[AS3] Awyong, P. W., Scott, P. R., Circumradius – diameter and width – inradius relations for lattice-constrained convex sets, Bulletin of the Australian Mathematical Society 59 (1999) 147 – 152.

[C] Croft, H. T., Cushions, cigars and diamonds: an area – perimeter problem for symmetric ovals, Mathematical Proceedings of the Cambridge Philosophical Society 85 (1979) 1 – 16.

[E] Ehrhart, E., Une généralisation du théorème de Minkowski, Comptes Rendus 240 (1955) 483 – 485.

[EH] Elkington, G. B., Hammer, J., Lattice points in a convex set of given width, Journal of the Australian Mathematical Society (A) 21 (1976) 504 – 507.

[H] Hammer, J., Volume – surface area relations for n-dimensional lattices, Mathematische Zeitschrift 123 (1971) 219 – 222.

[HCG] Hernandez Cifre, M. A., Gomis, S. S., Some inequalities for planar convex sets containing one lattice point, Bulletin of the Australian Mathematical Society 58 (1998) 159 – 166.

[HCG2] Hernandez Cifre, M. A., Gomis, S. S., Some area – diameter inequalities for two dimensional lattices, Geometriae Dedicata 72 (1998) 325 – 330.

[M] Minkowski, H., Geometrie der Zahlen, Teubner, Leipzig (1891).

[S] Scott, P. R., On planar convex sets containing one lattice point, Quarterly Journal of mathematics Oxford (2) 36 (1985) 105 – 111.

[S2] Scott, P. R., A bounded ness condition for sets with lattice point constraints, Bulletin of the Australian Mathematical Society 28 (1) (1983) 5 – 8.

[S3] Scott, P. R., Lattices and convex sets in space, Quarterly Journal of mathematics Oxford (2) 36 (1985) 359 – 362.

[S4] Scott, P. R., On the area of planar convex sets containing many lattice points, Bulletin of the Australian Mathematical Society 35 (3) (1987) 441 – 454.

[S5] Scott, P. R., Properties of axial diameters, Bulletin of the Australian Mathematical Society 39 (3) (1989) 329 – 334.

[SA] Scott, P. R., Awyong, P. A., Inequalities for convex sets, Journal of Inequalities in Pure and Applied mathematics 1 (1) Article 6 (2000). http://jipam.ve.edu.au .

[Sch] Schaeffer, J. J., A smallest lattice point covering convex set, Mathematische Annalen 129 (1955) 264 – 273.

[V] Vassallo, S., A covering problem for plane lattices, 43 (1992) 321 – 335.