For those with some calculus ...

In order to place the lines of latitude on Mercator’s map, we need the result:

If is the general angle of latitude, and R the radius of the earth, then the distance D(') of the line of latitude ' from the equator on Mercator’s map is
                      

Exercise 1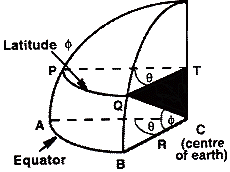 

Use this diagram to obtain Wright’s result as follows. Show that arc AB has length R and that arc PQ along latitude has length (Rcos ).. Now, how much must length PQ be stretched?
                                                        Check

In 1645, Henry Bond established that
              D(') = – R ln tan [1/2.(/2 – ')].
Bond’s unpleasant looking result allowed Mercator’s map to be produced to any desired accuracy, a boon to navigators ever since.
Exercise 2

Use differentiation to verify that
           sec x dx = – ln tan [1/2.(/2 – x)].
As usual, ‘ln’ is the natural logarithm. This exercise is in fact easier than it first appears!

                               Check    
The circle of radius R has perinmeter 2R. Hence arc AB will have length
(/2).2R = R.

Now arc PQ has radius
Rsin(/2 –) = Rcos.
So arguing as above, arc PQ will have length (R.cos).

So PQ must be enlarged by a factor sec =1/cos.
Differentiating the right hand side, using the chain rule gives

– 1/ tan [1/2.(/2 – x)].sec2 [1/2.(/2 – x)].(–1/2)

= + 1/{ 2 sin [1/2.(/2 – x)].cos [1/2.(/2 – x)]}

= 1/ sin (/2 – x) = 1/ cos x = sec x

as required.