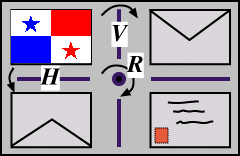
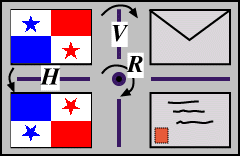
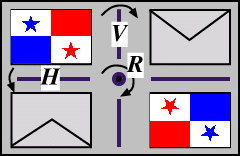
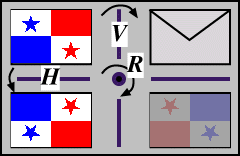
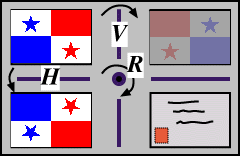
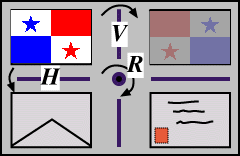
We have seen that the (non-square) rectangle has just four symmetries: I, V, H and R. We find that we can actually set up an algebraic structure of these symmetries, in the sense that one symmetry followed by another gives rise to a symmetry in the set. We shall illustrate these combinations of symmetries of the rectangle, using a flag for demonstration (in much the same as we used the envelope previously). Click successively on two of the rectangles at left below. There are 16 cases to investigate!