3. INFINITE COASTLINE, BUT HOW MUCH LAND? Minkowski Island, Area, Perimeter, Isoperimetric Problem

1. Area 2. Areas by direct measurement 3. The Minkowski Island 4. The Logo program 5. Area, perimeter  6. Isoperimetric problem 7. Further investigations

Area The area of a square is simply the square of the length of one side. The area of a rectangle is also easy: breadth height. Not all areas are so easy. The areas of some figures, such as triangles, circles and parallelograms can be worked out mathematically, and you may already know the formulae for them. 1. The picture shows a rectangle R and a parallelogram S. The area A(R) of the rectangle ABCD is easily found:           A(R) = AB BC. Can you find a similar formula for the area of the parallelogram? Can you explain why this formula holds? In fact the two shapes have the same area. The area of the parallelogram is given by           A(S) = AB BC.

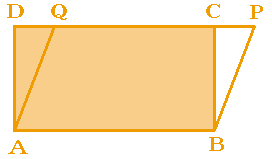We can see why this from the diagram. To turn the rectangle into the parallelogram, we remove triangular region ADF and add region BCE. These two triangles are congruent, i.e., they have the same shape and size, and so the same area (can you prove this?). We have given and taken away the same amount, so the area remains the same. Remember this idea; it will be useful later on.

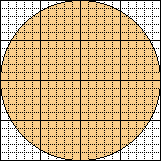
Areas by direct measurement We can approximate the area of irregular shapes by drawing the shape over a grid of squares, and counting the squares that fall inside the shape. Squares that lie on the border (that is, partly inside and partly outside the shape) are a difficulty. We may decide to count squares that appear to lie more inside the shape than outside it. 2. See how this works with a circle. The picture shows a circle drawn on a grid. The small dotted squares on the grid are of unit size. The solid squares are 5 5. Estimate the area of the circle by counting the large squares, then by counting the small squares. Fill in the table opposite. Compare your estimates with the true area of the circle. The circle has radius R = 10, and the area can be found using the formula:          Area of circle = R2.

Grid square size Estimated area 5 5 1 1

The Minkowski Island We can apply all these ideas about area to a fractal shape called the Minkowski Island. Like the Koch Island, the Minkowski Island is best approached in stages. We begin at level 0 with a simple square. Level 1 is obtained by replacing each side of the square with the pattern of eight congruent line segments (two of which are end to end in line) shown in the top part of the diagram. The complete island at this level is shown in the bottom of the diagram. The small arrows show the corners of the original square. To get to the next level, each line segment is replaced with the same pattern at a smaller scale. On the next screen is a Logo procedure that draws a Minkowski Island of size 100 and level 3. You will find that it contains two procedures: MSide : replaces a line segment with eight small segments (top diagram); MinkowskiIsland : draws a ‘square’, but instead of drawing a straight line for each side, it calls the MSide procedure.

Run the program and verify that the level 0 island is a square, and that the level 1 island is the shape shown in the diagram above. What do you think will happen as the level increases? The diagram adjacent to the program shows the level 3 island. The shape becomes more complex very quickly as the level increases.

The Logo program to MinkowskiIsland :size :level repeat 4 [MSide :size :level rt 90] end to MSide :size :level if :level = 0 [fd :size stop] MSide :size / 4 :level - 1 lt 90 MSide :size / 4 :level - 1 rt 90 MSide :size / 4 :level - 1 rt 90 MSide :size / 4 :level - 1 MSide :size / 4 :level - 1 lt 90 MSide :size / 4 :level - 1 lt 90 MSide :size / 4 :level - 1 rt 90 MSide :size / 4 :level - 1 end pu setx -75 sety 50 seth 90 pd MinkowskiIsland 100 3

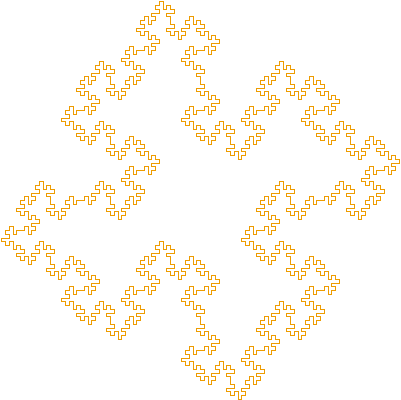Minkowski Island, Level 3

Area, perimeter of the Minkowski Island Q. What is the area of the Minkowski Island? Start with a unit square. 3. (a) Draw the Minkowski Island of level 0. What is its area? (b) Now look as we change the square to a level 1 island. Four small squares are removed from the original area, and four more are added. What is the area of the level 1 island? The small squares which are added and removed all have the same size, so there is no change in area. What happens at higher levels? Again, for each tiny square removed from the island, another of the same area is added. We thus obtain the surprising result: The area of the Minkowski Island, based on a unit square, is always 1, independent of the level.

We can find the perimeter of the Minkowski Island as we did for the Koch Island. What do you think it will be? 4. (a) The level 0 Minkowski island is the unit square. What is its perimeter? (b) Now draw one side of the level 1 island. What is its length? the perimeter of the level 1 island? (c) Draw up a table of perimeters for the various levels. What happens to the perimeter as the level increases? Level Perimeter 0 4 1 8 2 3 4 5 So, as the level increases, the perimeter keeps doubling but the area stays the same. The Minkowski Island, at level infinity, has infinite perimeter and finite area. The Koch Island has the same property.

The isoperimetric problem What we have been doing with perimeters and areas relates closely to a famous problem in geometry called the isoperimetric problem. Don’t be put off by the name; ‘isoperimetric’ simply means ‘with the same perimeter’. The problem is to find, among all the shapes with a given perimeter, the one with the greatest area. Before we start looking, what shape do you think it will be? This problem has a long history, and many mathematicians have tried to solve it. Many interesting approaches to the solution have been devised. To begin with, it is fairly easy to see that the shape we are looking for must be convex (that is, its borders should have no ‘hollows’).

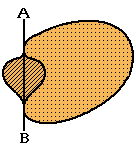
Suppose, as in the diagram, we have a shape (dotted) that is not convex. We draw a line across the hollow (line AB) and reflect the hollow section of the shape around this line. The new shape has the same perimeter as the old one, but has greater area. The striped area has been added. It is possible to show that the solution to the isoperimetric problem is a circle. The solution is perhaps intuitively obvious, but a logically rigorous proof is not trivial.

Further investigations 5. Trace a map of Australia on to graph paper. Determine (from the scale of the map and the size of the squares) the area represented by each square. Count the squares and estimate the area of Australia. 6. No matter how accurate your map of Australia in Question 5, and no matter how fine your grid, the answer will not be exact. There are two quite different reasons for this; what are they? 7. (Harder) See if you can work out the area of the Koch Island at various levels. The problem is not as simple as for the Minkowski Island, as the Koch Island does increase in area as the level increases. It will help you to know that the area A(T) of an equilateral triangle with sides of length L is                      A(T) = 3 L2/4.

8. Do this soap film demonstration of the isoperimetric problem. Use a loop of wire to make a flat film. Embed a small loop of cotton thread in the film. So long as the film is unbroken both inside and outside the cotton loop, the loop will be of arbitrary shape. Break the film inside the cotton, and it will immediately take on a circular shape, because the tension in the surrounding film is balanced when the cotton encloses a maximum area. 9. Think about why soap bubbles and planets are (approximately) spherical.