A Brief History of Non-Euclidean Geometry |
| Introduction
Euclid
Saccheri
Gauss/Bolyai
Lobachevsky
Riemann/Klein INDEX |
The next example of what we could now call a ‘non-euclidean’ geometry was given by Riemann. A lecture he gave which was published in 1868, two years after his death, spoke of a ‘spherical’ geometry in which every line through a point P not on a line AB meets the line AB. Here, no parallels are possible. 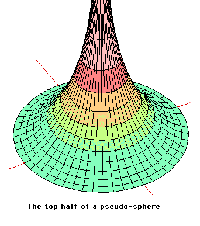 Also, in 1868, Eugenio Beltrami wrote a paper in which he put forward a model called a ‘pseudo-sphere’. The importance of this model is that it gave an example of the first four postulates holding but not the fifth. From this, it reduced the consistency of non-euclidean geometry to that of euclidean geometry.In 1871, Klein completed the ideas of non-euclidean geometry and gave the solid underpinnings to the subject. He showed that there are essentially three types of geometry. That proposed by Bolyai and Lobachevsky, where straight lines have two infinitely distant points. The Riemann ‘spherical’ geometry, where lines have no infinitely distant points and Euclidean geometry, where for each line there are two coincident infinitely distant points. < Prev |