 Another mathematician, Lobachevsky, worked on the same problems as Gauss and Bolyai but again, despite working at the same time, he knew nothing of their work. Lobachevsky also assumed the fifth postulate was not nessecary and from this formed a new geometry. In 1840, he explained how this new geometry would work, Another mathematician, Lobachevsky, worked on the same problems as Gauss and Bolyai but again, despite working at the same time, he knew nothing of their work. Lobachevsky also assumed the fifth postulate was not nessecary and from this formed a new geometry. In 1840, he explained how this new geometry would work,
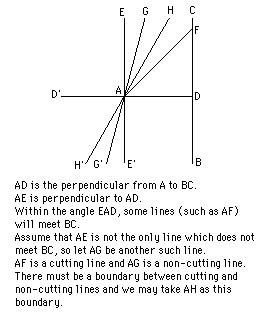
All straight lines which in a plane go out from a point can, with reference to a given straight line in the same plane, be divided into two classes – into cutting and non-cutting. The boundary lines of the one and the other class of those lines will be called parallel to the given line.
From this, Lobachevsky’s geometry has a new fifth postulate, that is
There exist two lines parallel to a given line through a given point not on the line.
Clearly, this is not equivalent to Euclid’s. Lobachevsky went on to develop many trigonometric identities for triangles which held in this geometry, showing that as the triangle becomes small the identities tend to the usual trigonometric identities. |
 Another mathematician, Lobachevsky, worked on the same problems as Gauss and Bolyai but again, despite working at the same time, he knew nothing of their work. Lobachevsky also assumed the fifth postulate was not nessecary and from this formed a new geometry. In 1840, he explained how this new geometry would work,
Another mathematician, Lobachevsky, worked on the same problems as Gauss and Bolyai but again, despite working at the same time, he knew nothing of their work. Lobachevsky also assumed the fifth postulate was not nessecary and from this formed a new geometry. In 1840, he explained how this new geometry would work,