

| Links |
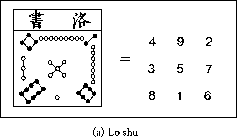
Although they are of little mathematical use, magic squares are an important aspect of ancient Chinese mathematics. Legend has it that magic squares were discovered in around 2200 BC by the Chinese Emperor Yu, who first saw it decorated upon the back of a divine tortoise along the banks of the Yellow River. It is a square array of numerals indicated by knots in strings, as shown below:



Note that there are black knots for the even numbers (representing yin) and white knots for the odd numbers (representing yang).
This square was considered to be magical as it was recognised that the sum of the numbers in every row, column, and in each of the major diagonals was the same. In the above magic square, for example, all of the rows, columns, and diagonals add up to 15.
Magic squares were not studied extensively mathematically until the 15th Century. In 1460, Emmanuel Moschopulus recognised that if the square n rows long and n columns wide, and the integers in the square were the numbers from 1 to n2, then the numbers in any row, column or diagonal add to n.(n2+1) /2. Such a square is called a magic square of order n.
Magic squares are still considered good luck charms in many parts of the world. Engraved on a silver plate, they were often prescribed as a charm against the plague, and were used as decorations of fortune telling bowls and amulets.