
Despite its name, Pascal’s Triangle was known to the Chinese as early as the twelfth century, around five centuries before the time of Pascal. It is used as a means of generating binomial coefficients and as such, once methods for solving quadratic and cubic equations were known, was used to generalise these methods to higher roots.
Jia Xian, who lived in the eleventh century, is attributed with writing the triangle out to the 6th row, and identifying the method we know today of generating it: A given element of the triangle is found by adding together the two values above it:

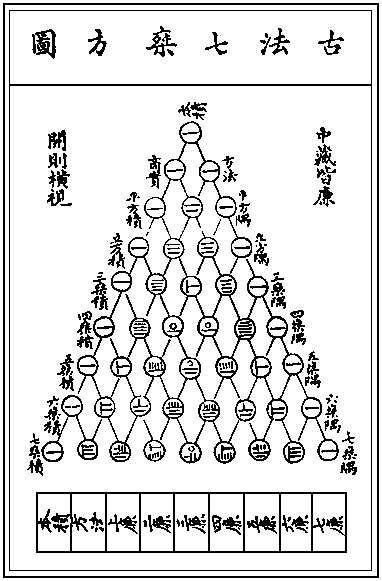
Yang Hui provided the first known presentation of the Pascal’s Triangle in 1261, written to depth 6, and it was later depicted by Chu Shikre in 1303 to depth 8, as shown below:
Pascal’s Triangle exhibits a number of interesting properties: For example, the elements in the nth row sum to 2n – 1, and if the first number of a row after the 1 is prime, then all of the numbers in that row (excluding the 1 s) are multiples of that prime.