Gauss’s Contribution
In his article 329 Disquisitiones Arithmeticae (1801), the German mathematician Carl Friedrich Gauss (1777 – 1855) wrote:
“The problem of distinguishing prime numbers from composite numbers and of resolving the latter into their prime factors is known to be one of the most important and useful in arithmetic. It has engaged the industry and wisdom of ancient and modern geometers to such an extent that it would be superfluous to discuss the problem at length ... . Further, the dignity of science itself seems to require that every possible means be explored for the solution of a problem so elegant and so celebrated.”
One of the most intriguing aspects of primes is that there is no obvious pattern governing their distribution among the positive integers. In fact all attempts to find a formula that will produce only primes, or even predict their exact distribution, have so far failed. But Gauss switched his attention from finding individual primes to finding their average distribution.
In 1792, at the age of 15, Gauss examined a table of prime numbers compiled by the German-Swiss Mathematician Johann Heinrich Lambert (1728 – 1777). Gauss was seeking a rule which governs the number of primes less than or equal to some integer x. We denote this number by p(x). For example since there are 6 primes smaller than 14, wehave p(14) =6. A closer examination indicates
that on average the gaps between primes becomes larger
and larger. Gauss asked whether for large x the behaviour of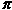 
(x) could be approximated by a known function. Gauss then made a bold conjecture which he scribbled on the back of his table of logarithms. It read
primzahlem unter 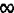a ( =
)
a/ln a.
This can be interpreted as saying
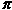(a) ~ a/ln a for
large values of a.
Gauss did not attempt to prove his conjecture, he merely got a sense of what he thought the answer should be. The proof (of the more precise result involving limits) eluded many great minds including Georg Friedrich Bernhard Riemann (1826 –1866), himself a student of Gauss, who published a paper on the subject in 1859. Success finally came in 1896 when Jacques Salomon Hadamard (1865 – 1963) of France and Charles de la Vallée-Poussin (1866 –1962) of Belgium independently proved Gauss’s conjecture. Today this result is known as The Prime Number Theorem.