The Four Colour Problem
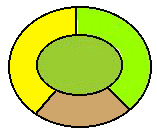
Since drawing a graph divides the plane into separate regions, it can be asked (which it was by Möbius in 1850, and popularized by Cayley in 1879): ‘How many colours are sufficient to colour all regions so that no two adjacent regions have the same colour?’
This is the famous Four Colour Problem which occupied mathematicians for over a century. Four colours are certainly required (see figure), but were four colours always enough? Progress was slow. By 1946, de Backer showed that four colours are sufficient to colour up to 35 regions, and Reynolds extended this to 83 regions by 1950. The problem was finally solved by Appel and Haken in 1976, with a computer proof based on graph theory.
