Königsberg

Salesman

Theory

Four Colours

Recent applications

Planar graphs

Links

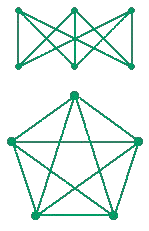Planar graphs

Another graph problem is that of finding all paths between three houses and three wells so that no paths cross. A few minutes’ doodling will convince you that it is impossible. The associated graph (top right) is said to be non-planar. (A planar graph is one in which no lines cross.) The graph below is also non-planar, while all Schlegel diagrams are planar.

In 1930, Kuratowski (left) showed that any graph is planar if and only if it does not have a subgraph equivalent to either of the adjacent graphs. Proving that a graph is planar is not very easy, and for large graphs requires a computer. Planar graphs are essential in designing printed circuit boards in electronics, because they allow the circuits to be printed on a single sheet of material, thus reducing size and cost.