2. ANALYTIC FUNCTIONS 
|
|
|
Functions of a Complex Variable
|
|
|
Let D be a subset of C. A function f : D  C is a rule that associates with each z in D a unique complex number w. We write w = f(z). C is a rule that associates with each z in D a unique complex number w. We write w = f(z).
Notes
1. The set D of numbers that are mapped is called the domain of f. Notice that we now have a double use of this word. Where the domain is unspecified, we assume it to be the largest subset of C for which f(z) is defined.
2. The set of image elements {w | w = f(z)} is called the range or image of the function.
3. The above definition specifies a unique image for each z  D. Later we shall extend this definition to include multivalued functions. D. Later we shall extend this definition to include multivalued functions.
| Example 1. f(z) = z2 + iz – 3. The domain is C.
f(z) = 1/(1 + z2). Here the domain is C \ { i}. i}.
|
If f(z) only assumes real values, f is real-valued.
| Example 2. f(z) = |z|, f(z) = Re z = x, f(z) = Im z = y. |
We can break w = f(z) into real and imaginary parts. Thus if w = u + iv, z = x + iy, then
w = f(z) = u(x, y) + iv(x, y)
| Example 3. f(z) = z2.
Here u + iv = (x + iy)2 = (x2 – y2) + 2ixy, so u = (x2 – y2), v = 2xy.
|
This expression in terms of real and imaginary parts may be easier said than done! In theory, it allows us to deduce properties of complex functions from our knowledge of the real numbers.
A real function y = f(x) can be represented geometrically by a graph: the set of points {(x, y) | y = f(x)}. To represent the complex function w = f(z) geometrically, in general we need four dimensions or two planes: a plane for the domain, and a plane for the range. For simple functions, we can use the same plane twice.
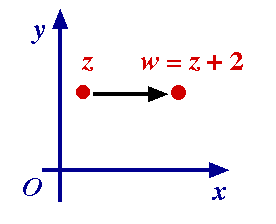 Example 1. w = f(z) = z + 2. Example 1. w = f(z) = z + 2.
This is a translation:
each point z is translated through 2 to the point z + 2.
|
|
|
Mapping Curves and Regions
|
 |
 |
We shall be mapping curves and regions rather than just points.
| Example
Find the image of the circle x2 + y2 = c2 (c > 0) under w = f(z) =  (x2 + y2) – iy. (x2 + y2) – iy.
Let us set w = u + iv. Then each point (x, y) on the circle x2 + y2 = c2 maps to (u, v) = (c, –y), where |y|  c. c.
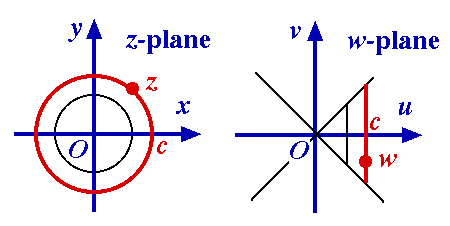 Thus the image of this circle is the line segment u = c, –c Thus the image of this circle is the line segment u = c, –c  v v c in the uv-plane. c in the uv-plane.
The domain of f is the z-plane; the range of f is a quadrant of the w-plane.
Notice that z = (x, y) and –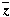 =(–x, y) map to the same point w. =(–x, y) map to the same point w.
|
All work on functions of two variables now carries over directly. A minor difference is that because we are dealing with complex numbers, the length or norm of a vector represented by w becomes the modulus |w| of w.
Thus the definition of limit becomes:
=w.gif) means means
for all  > 0, there exists > 0, there exists 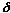 > 0 : for all z, 0 < |z – z0| < > 0 : for all z, 0 < |z – z0| < 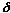  |f(z) – w0| < |f(z) – w0| <  . .
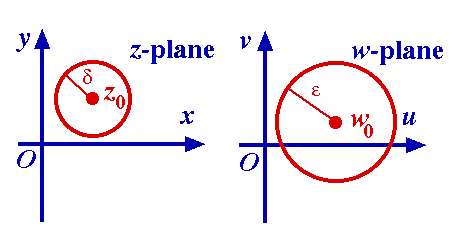
Thus every z in the left disc has an image in the right disk. We may not obtain the whole of the right disc; for example, consider the image of f(z) = constant = w0 : this is just the central point of the second disk
Theorem 2.1 If w = f(z) = u + iv, z = x + iy, z0 = x0 + iy0, then
(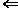 ) Now let us suppose that ) Now let us suppose that 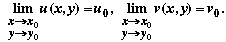
Then there exist 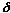 1 > 0, 1 > 0, 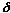 2 > 0 such that 2 > 0 such that
0 < |x – x0| < 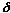 1, 0 < |y – y0| < 1, 0 < |y – y0| <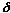 1 1  |u(x, y) – u0| < |u(x, y) – u0| <  /2, /2,
0 < |x – x0| < 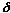 2, 0 < |y – y0| < 2, 0 < |y – y0| <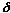 2 2  |v(x, y) – v0| < |v(x, y) – v0| <  /2, /2,
Choose 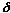 = min( = min(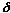 1, 1, 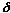 2). Then using the given limits, 2). Then using the given limits,
0 < |(x – x0) + i(y – y0)| < 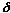 
|(u(x, y) + iv(x, y)) – (u0 + iv0)|  |u(x, y) – u0| + |i| |v(x, y) – v0| < |u(x, y) – u0| + |i| |v(x, y) – v0| <  /2 + /2 +  /2 < /2 < . .
Our previous theorem quickly leads to the well-known and useful Limit Theorems. We use an easy to remember abbreviated notation.
Theorem 2.2. (Limit Theorems) If lim f, lim g exist, then
lim (f g) = lim f g) = lim f  lim g lim g
lim (f . g) = lim f . lim g
lim (f / g) = lim f / lim g (lim g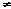 0) 0)
Proof (a) Set f = u + iv, lim f = u0 + iv0, g = U + iV, lim g = U0 + iV0. Now
lim (f + g) = lim (u + U + i(v + V)) (substitute and rearrange)
= lim (u + U) + i lim(v + V) (Thm 2.1)}
= u0 + U0 + i(v0 + V0) (put in the limits)
= (u0 + iv0) + (U0 + iV0) (rearrange)
= lim f + lim g.
The other proofs are similar.
Definition Function f is said to be continuous at z0 if f satisfies the following three conditions.
(a) f(z0) exists ; (b) lim z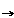 zo f(z) exists ; (c) lim z zo f(z) exists ; (c) lim z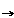 zo f(z) = f(z0). zo f(z) = f(z0).
Notes
1. Just writing statement (c) assumes the truth of (a) and (b).
2. Expressing (c) in terms of the limit definition, we obtain:
This is slightly different from the usual definition of limit, in that we allow the possibility z = z0 (omitting 0 < |z – z0| ... ).
Function f = f(z) is said to be continuous in a region if it is continuous at each point of the region.
|
|
Properties of Continuous Functions
|
 |
 |
The sum f + g, difference f – g, product f.g and quotient f/g of two continuous functions is continuous at a point z = z0, with the proviso that in the last case g(z0)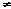 0. These results follow directly from the Limit Theorems 2.2. 0. These results follow directly from the Limit Theorems 2.2.
| Examples
1. Polynomial functions The polynomial function P(z) = 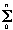 ai z i is continuous forall z since it is constructed as sums and products of the continuous constant functions (ai) and the continuous function f(z) = z. ai z i is continuous forall z since it is constructed as sums and products of the continuous constant functions (ai) and the continuous function f(z) = z.
2. Rational functions The rational function P(z) / Q(z) given by the quotient of two continuous polynomial functions P(z), Q(z) is continuous for all z : Q(z) 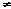 0. 0.
|
|
|
Composition of Continuous Functions
|
 |
 |
We can also compose complex functions f, g to obtain the new function f o g defined by (f o g)(z) = f(g(z)). If f, g are continuous, will f o g be continuous also?
Theorem 2.3 The composite function f o g of two continuous functions f, g is continuous.
Alternatively, a continuous function of a continuous function is a continuous function. Formally, the proof of this theorem is exactly as for the real case, and is omitted here.
| Example f(z) = sin (z2) is continuous for all z. |
By Theorem 2.1, f(z) = u + iv is continuous  u(x, y), v(x, y) are continuous. Thus: u(x, y), v(x, y) are continuous. Thus:
| Example f(z) = exy + i sin(x2 – 2yx3) is continuous for all z (since the real and imaginary parts are continuous). |
Definition Say f is bounded in region R if |f(z)|  M for all z M for all z 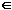 R. R.
If f is continuous in R, then f is bounded because of the corresponding properties of u, v. Show this!
Formally, the definition of the derivative f '(z) for functions of a complex variable is the same as for real functions.
Let f be a function whose domain contains a neighbourhood of point z0. Then
if the limit exists. In this case the function f is said to be differentiable at z0.
It is sometimes preferable to use the alternative form of the derivative obtained by setting z = z0 + 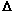 z : z :
Note Since z0 lies in an (open) neighbourhood of the domain of f, f(z0 + 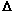 z) is defined if z) is defined if 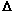 z is small. z is small.
|
|
Examples of the Derivative
|
 |
 |
We can evaluate simple derivatives by using the basic definition.
The usual differentiation formulae hold as for real variables.
For example, 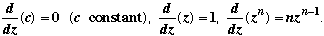
However, care is required for more unusual functions.
Example f(x) = |x|2 = x2  f'(x) = 2x for all x. f'(x) = 2x for all x.
But f(z) = |z|2  f '(z) exists only at z = 0. f '(z) exists only at z = 0.
|
This last statement is proved using the basic definition. Show it!
As in the real case, f is differentiable  f is continuous. f is continuous.
The same rules apply for the sum, product, quotient and composite of two differentiable functions (where defined).
Example 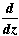 (2z2 + i)5 = 5(2z2 + i)4.4z = 20z(2z2 + i)4. (2z2 + i)5 = 5(2z2 + i)4.4z = 20z(2z2 + i)4. |
Again, with more unusual functions, we may have to use the limit definition of differentiation.
Example Investigate 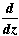 (Re z). (Re z).
We get 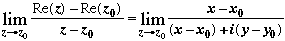
Here we get 0 approaching along x = x0, 1 along y = y0. Hence the limit does not exist.
|
|
|
Cauchy-Riemann Equations (I)
|
 |
 |
Theorem 2.1 gives us conditions for continuity for a function of a complex variable in terms of the continuity of the real and imaginary parts. We now ask: Is there any test for differentiability?
Theorem 2.4 The derivative f '(z) of f = u + iv exists at z  the first order partial derivatives ux, vx, uy, vy all exist and satisfy the first order partial derivatives ux, vx, uy, vy all exist and satisfy
ux = vy, uy = –vx (the Cauchy-Riemann equations).
Further, f '(z) = ux + ivx = vy – iuy.
Proof Since the derivative of f exists,
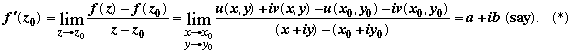
|
|
Cauchy-Riemann Equations (II)
|
 |
 |
By Theorem 2.1, lim Re(*) = a, lim Im (*) = b.
Set y 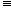 y0 to get y0 to get 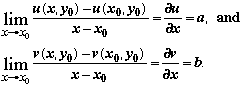
Set x 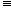 x0 to get x0 to get 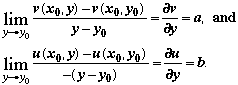
Hence all the first partial derivatives exist, ux = vy, uy = –vx, and
f '(z0) = ux(x0, y0) + ivx(x0, y0) etc. as required.
1. Set f(z) = z2 = (x + iy)2 = (x2 – y2) + 2ixy.
Now f'(z) = 2z exists for all z. So the Cauchy-Riemann equations are satisfied.
We have u = x2 – y2, v = 2xy, and ux = 2x = vy, uy = –2y = –vx.
Also f '(z) = ux + ivx = 2x + 2iy = 2z as expected.
2. Set f(z) = |z|2. We show f '(z) does not exist for z 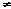 0. 0.
Now f(z) = x2 + y2, i.e. u = x2 + y2, v = 0, ux = 2x, uy = 2y, vx = 0 = vy.
So ux = vy  x = 0, uy = –vx x = 0, uy = –vx  y = 0. y = 0.
Hence f '(z) can only exist at (0, 0).
Does f '(0) exist? Yes; as suggested earlier; we must use a first principles argument.
Theorem 2.4 gives necessary conditions for f to be differentiable. We now seek sufficient conditions for f ' to exist: that is, a similar statement, but using 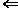 . .
Theorem 2.5 Let f = u + iv as before. Suppose that
(i) u, v, ux, vx, uy, vy exist in the neighbourhood of (x0, y0),
(ii) ux, vx, uy, vy are continuous at (x0, y0),
(iii) the Cauchy-Riemann equations are satisfied at (x0, y0).
Then f '(z) exists and at z0, f '(z0) = ux + ivx as before.
That is, f is differentiable at z0 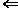 the given conditions. the given conditions.
Proof We omit this proof. It is not hard, but rather messy.
The real functions u = ex cos y, v = ex sin y are defined and continuous everywhere. So are ux, vx, uy, vy and you can easily check that the Cauchy-Riemann equations are satisfied.
Hence the function f(z) = ex cos y + i ex sin y is differentiable everywhere.
Since ux = u, vx = v,
f '(z) = f(z) ( = ex cis y = ex + iy = ez).
Definitions f(z) is analytic at z0 if f '(z) exists not only at z0 but for all z in some neighbourhood of z0. f(z) is analytic in a domain of the z-plane if it is analytic at every point of the domain. f(z) is entire if it is analytic everywhere.
| Examples
1. f(z) = |z|2 is not analytic anywhere. (It is in fact differentiable only at z = 0).
2. f(z) = 1/z is analytic (except at z = 0).
3. f(z) = a0 + a1z + ... + an zn is entire.
|
If f(z) is analytic throughout a domain except for a finite number of points, such points are singularities or singular points of f.
| Examples
f(z) = 1/z (z = 0 is a singularity);  (z = 1, 2 are singularities). (z = 1, 2 are singularities).
|
|
|
Test for Analytic Functions
|
 |
 |
equating real, imaginary parts to zero.
Hence f analytic  the Cauchy-Riemann equations hold the Cauchy-Riemann equations hold  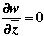 as required. as required.
|
|
Analytic Functions: Final Comments
|
 |
 |
| Example
We can say immediately that this function is not analytic, as x and y do not occur in the combination x + iy. In some examples it is less clear whether or not the variables can be combined in this way.
|
Derivative Theorems
The theorems on derivatives quickly transfer to analytic functions.
Thus the sum, product, quotient and composite of two analytic functions are formed in the obvious ways as before, and each of the resulting functions is analytic on its domain.
Let f = u + iv be analytic in some domain of z-plane. Then the Cauchy-Riemann equations hold:
It can be shown that for analytic function, the partial derivatives of all orders exist
and are continuous functions of x, y. Hence
uxx = vyx and uyy = –vxy.
Assuming continuity of vyx, vxy, we have vyx = vxy, and hence
This is Laplace's equation, and u is called an harmonic function. In the same way we get
vxx + vyy = 0; i.e. v is an harmonic function.
If f = u + iv, u and v are conjugate harmonic functions.
(Note the different use of the word ‘conjugate’ here).
|
|
Finding Conjugate Harmonic Functions
|
 |
 |
In applied mathematics (partial differential equations) we often seek an harmonic function on a given domain which satisfies given boundary conditions. If we are given one of two conjugate harmonic functions, it is a simple matter to find the other. We use the Cauchy-Riemann equations.
| Example
Let u = y3 – 3x2y. Then u is harmonic, since uxx = – 6y = – uyy.
Now using the Cauchy-Riemann equations, ux = –6xy = vy.
Integrating v partially with respect to y gives v = –3xy2 + 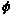 (x) and now (x) and now
vx = –uy = –3y2 +3x2  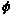 '(x) = 3x2. '(x) = 3x2.
Hence v = –3xy2 + x3 + c.
You can check that v is in fact harmonic! So
f(z) = (y3 – 3x2y) + i(x3 – 3xy2 + c) [= i(z3 + c) in fact].
|
|