|
STELLATIONS
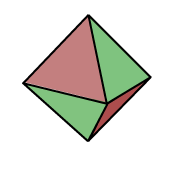
The word ‘stellation’ has an obvious connection to the word ‘stellar’. It means star shaped. We can illustrate how stellation occurs with the stella octangula which we have studied previously. We start with the regular octahedron. There are eight faces, each lying in a plane. Some of these planes meet again in pairs, extending beyond the faces themselves, and we obtain the stella octangula.
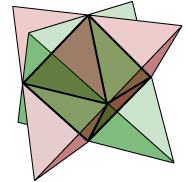
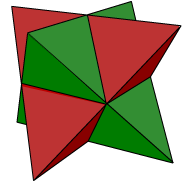
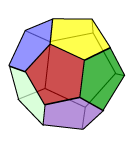
This process will not work if we start with a regular tetrahedron (there are no further lines of intersection), or the cube (the opposite faces are parallel). However, if we start with the regular dodecahedron, we find that there are three different stellations. We studied these previously. You can find them under small stellated dodecahedron, great dodecahedron, and great stellated dodecahedron. However, in summary we have:
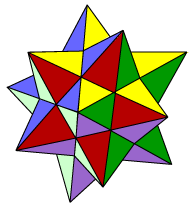
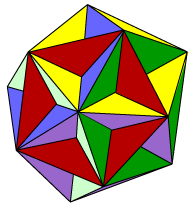
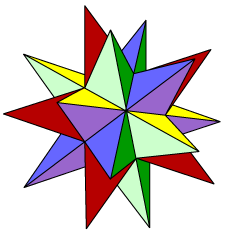
We first stellate the dodecahedron by extending each face in all directions, thus obtaining pentagram faces, and forming a pyramid on each original face pentagon. This gives rise to the small stellated dodecahedron. Next, working within those same face planes, each pentagram face of the small stellated dodecahedron is extended to become a regular pentagon. These intersecting pentagonal faces now bound the great dodecahedron. Finally, still working within the same face planes, each regular pentagonal face of the great dodecahedron is extended to form a larger pentagram. These pentagram faces now bound the great stellated dodecahedron. The process stops here: there are no further stellations. (We might expect large regular pentagons at the next step. But take the circumscribing pentagon of the blue star. Each edge would need to be the edge of another such pentagon. But none are available.)
We are ultimately interested in investigating the stellations of the icosahedron, which are many! Perhaps we can learn some techniques from the simpler dodecahedral case. By symmetry, the stellation diagram centred on every face of the basic dodecahedron will be the same.
Notice that although we tend to draw the various stellations about the same size, in their construction, they actually get larger and larger.
Coxeter, H. S. M., Introduction to Geometry, Wiley (1969). Coxeter, H. S. M., Regular Polytopes, Macmillan 2nd Ed. (1963). Dutch, Steven : http://www.uwgb.edu/dutchs/symmetry/stellate.htm Wenninger, M. J., Polyhedron Models, Cambridge (1979). |
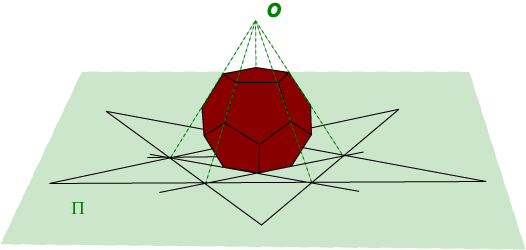
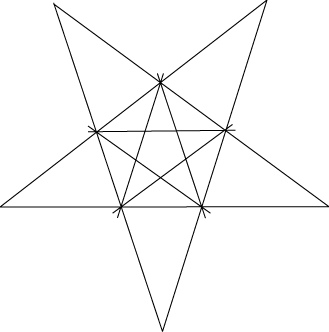 Since these lines designate exactly the possible ways in which the faces of the dodecahedron can impinge on this plane, the face pattern of any stellation will be contained within this shape. In fact, a suitable pattern is to colour in each polygonal shape which can actually be seen in the stellation. For example, for the basic octahedron, the stellation diagram would look like
Since these lines designate exactly the possible ways in which the faces of the dodecahedron can impinge on this plane, the face pattern of any stellation will be contained within this shape. In fact, a suitable pattern is to colour in each polygonal shape which can actually be seen in the stellation. For example, for the basic octahedron, the stellation diagram would look like